The Riddler — Can You Slay The Puzzle Of The Monsters’ Gems?

 

Had to take a break from last week’s Rid­dler, Can You Solve The Puz­zle of the Over­flow­ing Mar­ti­ni Glass, part­ly because I was short on time, but most­ly because I had a lot of trou­ble fig­ur­ing it out. My 17 year old broth­er and his friends were able to fig­ure it out, which was embar­rass­ing reminder of how much Calc I’d forgotten.

The Rid­dler is a week­ly puz­zle series from Oliv­er Roed­er at FiveThir­tyEight that usu­al­ly involves some com­bi­na­tion of math, log­ic and probability.

This weeks FiveThir­tyEight Rid­dler, Can You Slay The Puz­zle of the Mon­sters Gems was:

A video game requires you to slay mon­sters to col­lect gems. Every time you slay a mon­ster, it drops one of three types of gems: a com­mon gem, an uncom­mon gem or a rare gem. The prob­a­bil­i­ties of these gems being dropped are in the ratio of 3:2:1 — three com­mon gems for every two uncom­mon gems for every one rare gem, on aver­age. If you slay mon­sters until you have at least one of each of the three types of gems, how many of the most com­mon gems will you end up with, on aver­age?

Same with all the oth­er Rid­dlers, first thing I like to do is sim­u­late the prob­lem, since it’s gen­er­al­ly gives you a good start­ing point to the prob­lem, and pro­vides a way to check the solution.

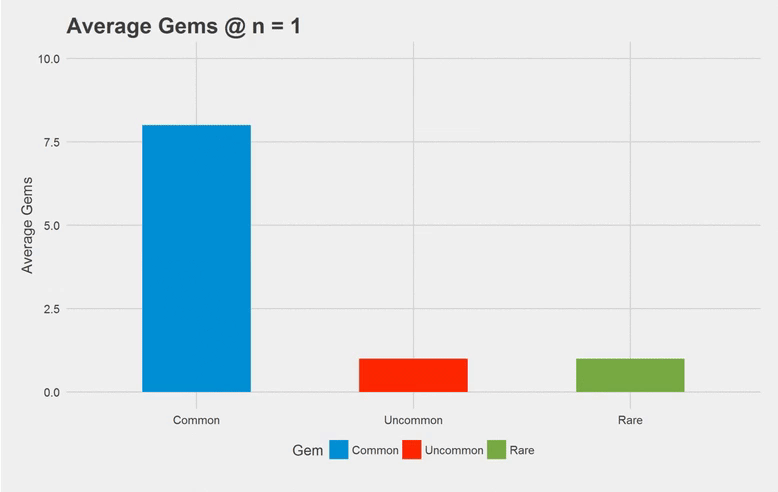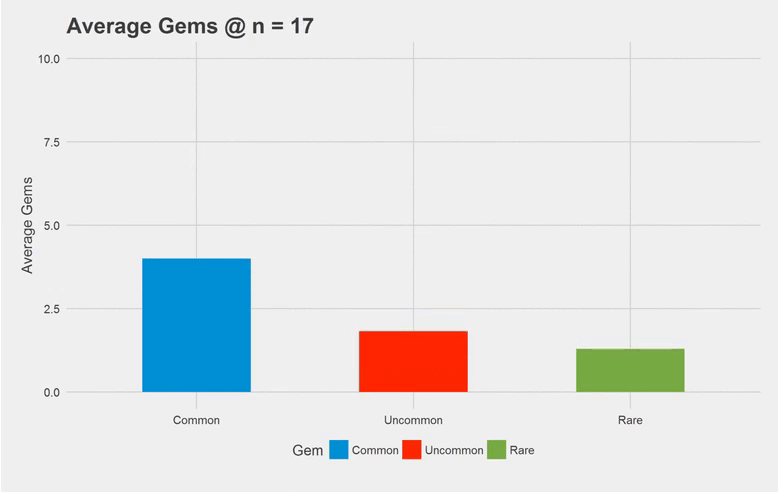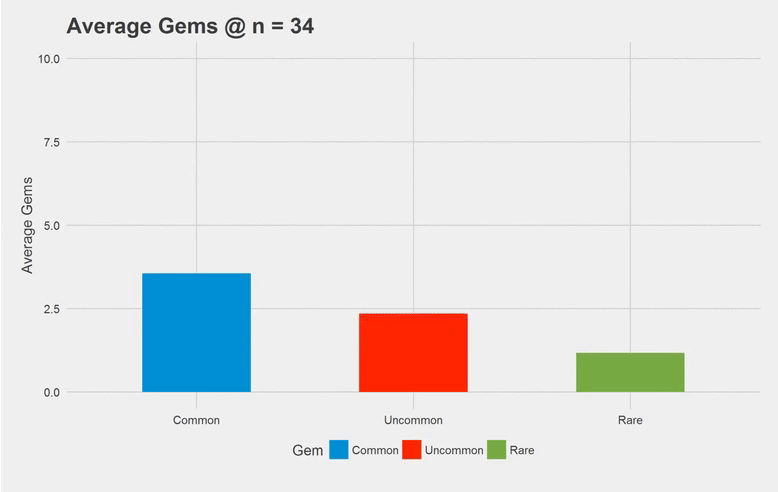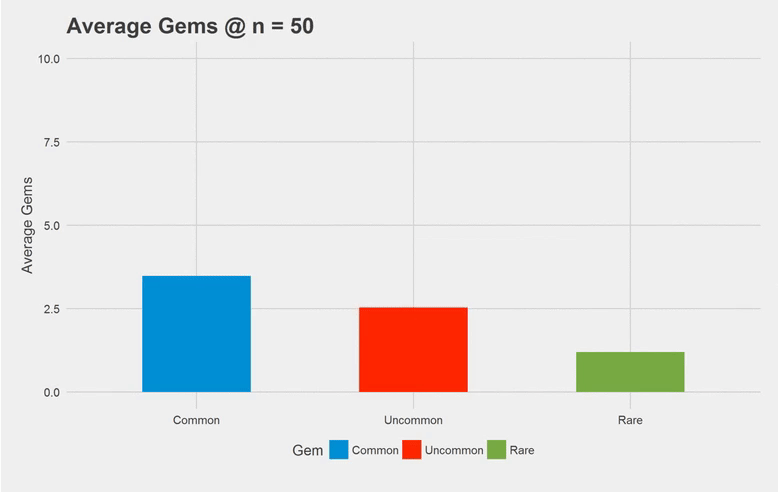
The above’s just a quick gif of the sim­u­la­tion out­put. I only went up to n = 50, since the aver­age gems does­n’t change much after n = 50. I found that the amount of com­mon, uncom­mon and rare gems we see when we have all the gems are rough­ly 3.6, 2.4 and 1.2 gems respec­tive­ly after a large amount of iter­a­tions (n =1000). That makes sense since that falls into the 3:2:1 prob­a­bil­i­ty we’re giv­en in the problem.

 

This prob­lem is actu­al­ly real­ly sim­i­lar to the famous Coupon Col­lec­tor prob­lem. It’s a lit­tle dif­fer­ent in that we deal with unequal prob­a­bil­i­ties. This can be dealt with the Max­i­mum-Min­i­mums Iden­ti­ty, (for­mu­la below) which is out­lined in Sec­tion 3.1 of The Coupon Col­lec­tors Prob­lem by Mar­co Fer­rante and Mon­i­ca Saltalamacchia.

We’ll start with the fol­low­ing variables:

E_mon­sters = Expect­ed # of Slayed Mon­sters to Col­lect All Gems

P_com­mon = Prob­a­bil­i­ty of Get­ting a Com­mon Gem = 1/2

P_uncom­mon = Prob­a­bil­i­ty of Get­ting an Uncom­mon Gem = 1/3

P_rare = Prob­a­bil­i­ty of Get­ting a Rare Gem = 1/6

The max­i­mum-min­i­mums equa­tion, for the sake of our prob­lem, is essentially:

E_mon­sters = [ E_{mon­sters for Com­mon gem} + E_{mon­sters for Uncom­mon gem} + E_{mon­sters for Rare gem} ] -

[ E_{mon­sters for Com­mon or Uncom­mon Gem} + E_{mon­sters for Com­mon or Rare gem} + E_{mon­sters for                                      Uncom­mon or Rare gem} ] +

[ E_{mon­sters for Com­mon, Uncom­mon, or Rare Gem} ]

Expect­ed mon­sters for each gem is just the rec­i­pro­col of the prob­a­bli­ty (E_{mon­sters for Uncom­mon gem} = 1/P_com­mon). The prob­a­bil­i­ty for E_{mon­sters for Com­mon or Uncom­mon Gem}  is also eas­i­ly calculated.

P_{com­mon, uncom­mon} = P_com­mon,  + P_uncom­mon  = 1/2 + 1/3 = 5/6

So our E_mon­sters equa­tion is:

E_mon­sters = [ 1/P_Com­mon  + 1/P_Uncom­mon  + 1/P_Rare] -

[ 1/P_{Com­mon, Uncom­mon}  + 1/P_Common,Rare  + 1/P_{Uncommon,Rare}] +

[ 1/P_{Com­mon, Uncommon,Rare}]

Plug in our val­ues and we get:

E_mon­sters = [2+3+6] — [6/5 + 3/2 + 2] + 1 = 11 — 4.7 + 1 = 7.3 Mon­sters to Slay to get all Gems

The ques­tion asks for expect­ed num­ber of com­mon gems when you’ve got­ten at least one every gem. That’s simply

E_mon­sters * P_Com­mon  = 7.3 * 1/2 = 3.65

An expect­ed val­ue of 3.65 Com­mon Gems is con­sis­tent with the val­ues we got from our sim­u­lat­ed experiment.