The Riddler – Alligators, Sharks, Bridges and Friends

It’s been a very long time since I’ve updat­ed this, and while some if it has been lazi­ness on my part, most of the blame can be blamed on North­west­ern EDI — an awe­some Mas­ter’s pro­gram I start­ed about 2 months ago (also the last time I post­ed an update). It’s been a great expe­ri­ence so far, and the pro­gram’s going to be the cat­a­lyst for a lot of the work I’ll be post­ing from here on out.

With­out fur­ther ado, The Rid­dler [Express].

For those that aren’t famil­iar, The Rid­dler is a week­ly puz­zle series from Oliv­er Roed­er at FiveThir­tyEight that usu­al­ly involves some com­bi­na­tion of math, log­ic and prob­a­bil­i­ty. The Rid­dler Express is a sim­pler ver­sion of the clas­sic Riddler.

 

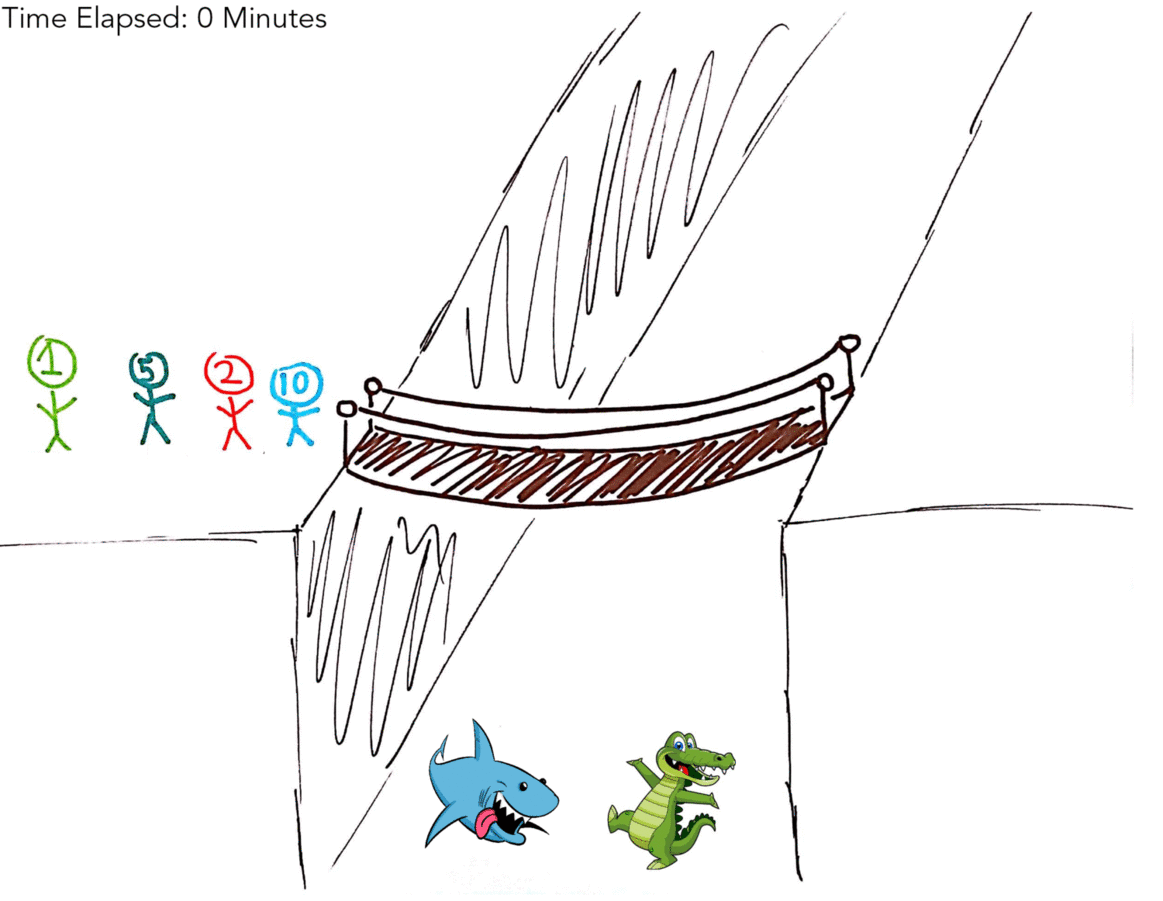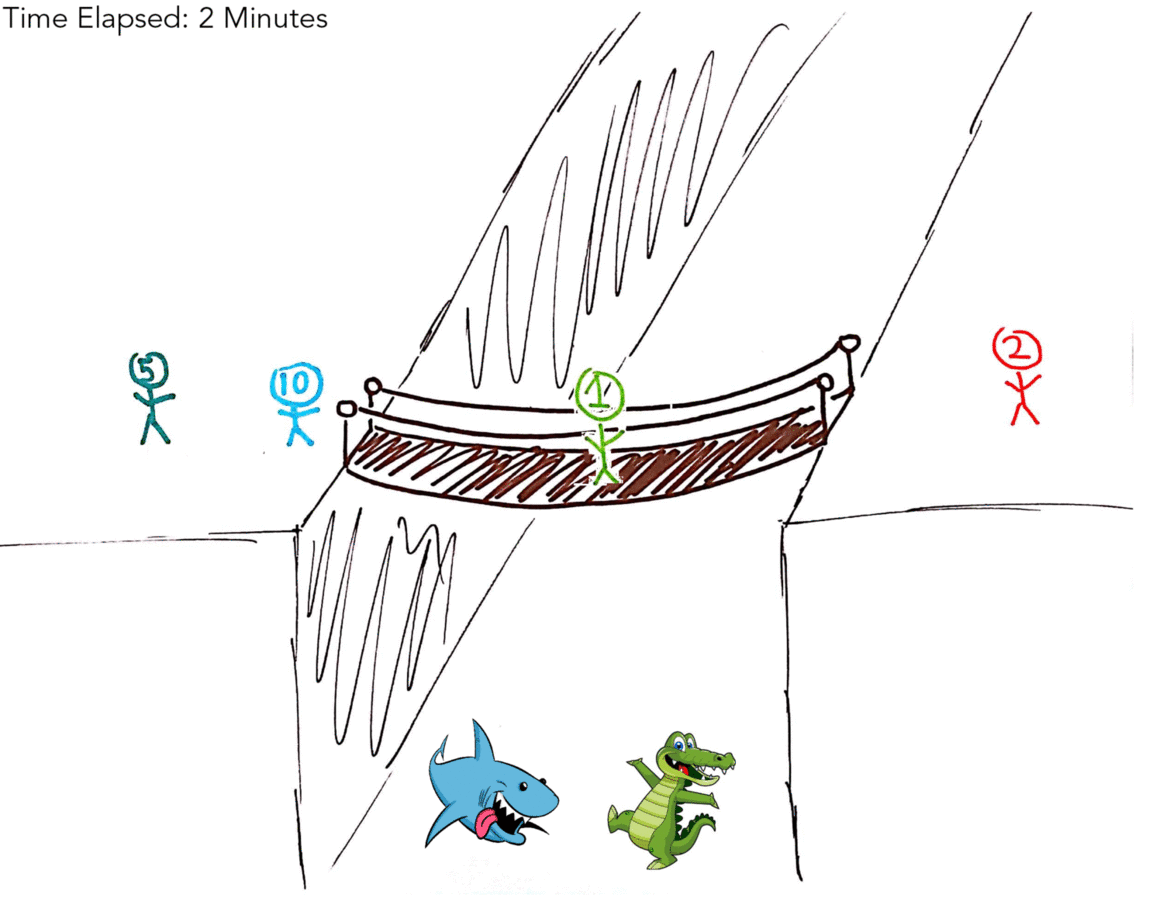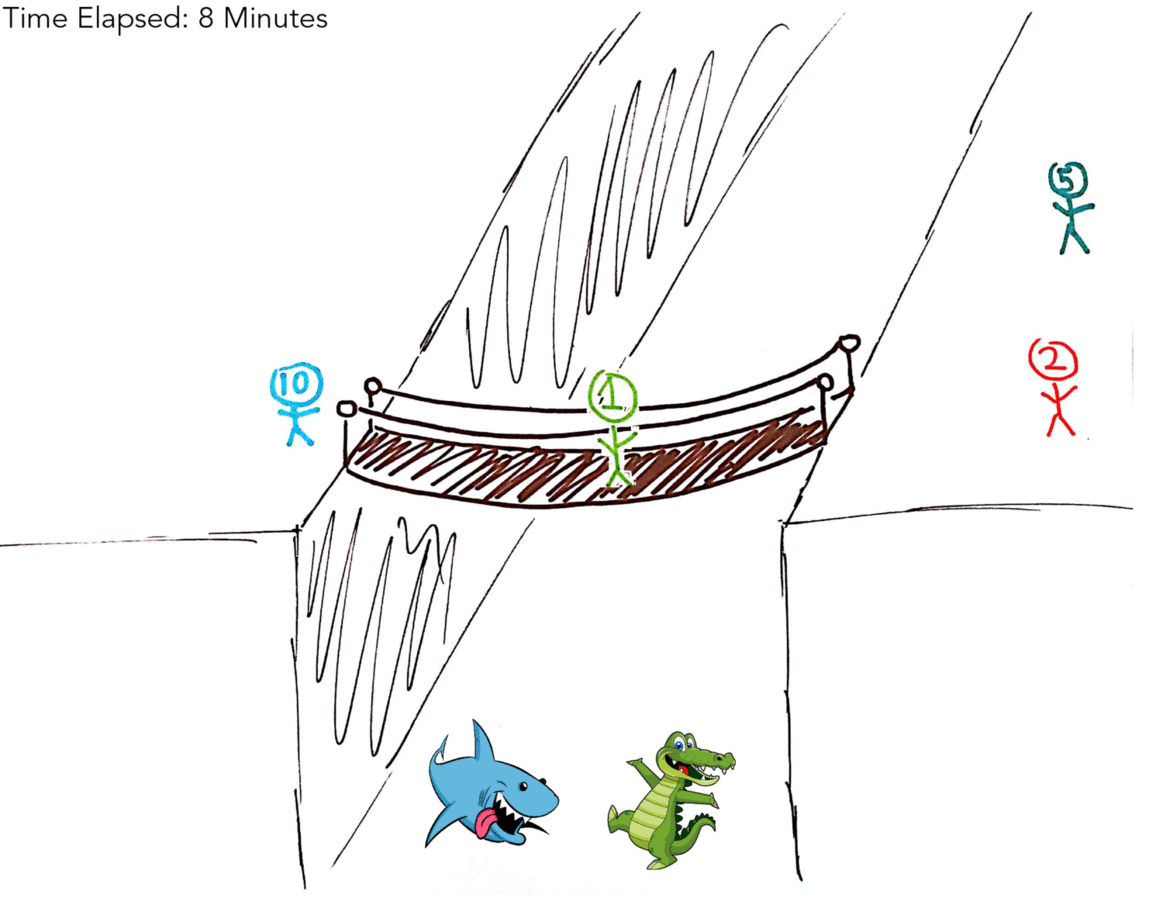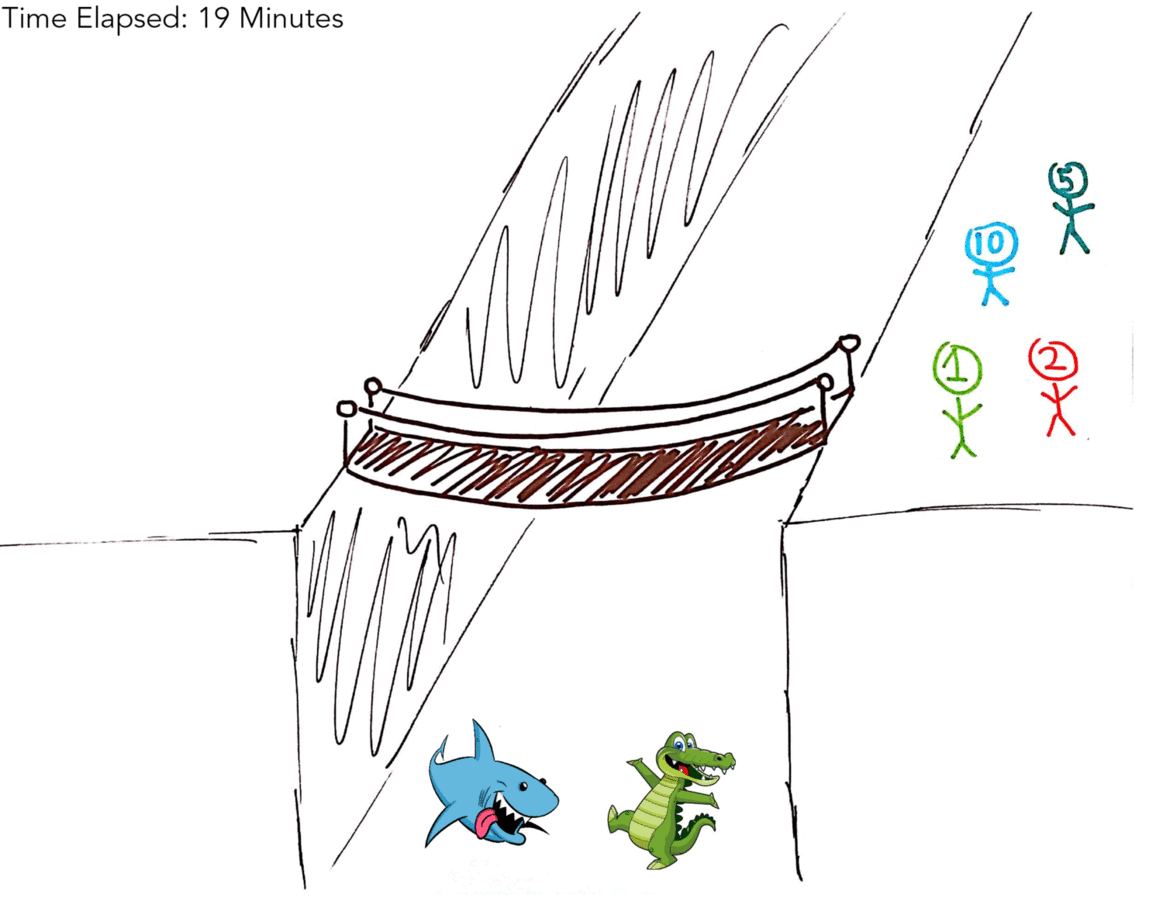
Four peo­ple have to cross an old, rick­ety bridge over deep, cold water infest­ed with sharks, alli­ga­tors, croc­o­diles and shriek­ing eels. The bridge is so old that it can hold no more than two peo­ple at any giv­en time. It’s the mid­dle of the night, so on every trip across the bridge, the per­son cross­ing needs to use the group’s only flash­light to cross safe­ly. The four peo­ple who need to cross all walk at dif­fer­ent speeds. One of them takes one minute to cross, one takes two min­utes, one takes five min­utes and one takes 10 min­utes. If two peo­ple cross togeth­er, they need to stay togeth­er to share the flash­light, so they cross at the speed of the slow­er per­son. For exam­ple, the one-minute per­son can cross with the 10-minute per­son, and that trip would take 10 minutes.

How quick­ly can all four peo­ple get across the bridge?

 

So your first thought, as mine was, might have been to include the 1 Minute man (here­by referred to as 1M) in every trans­ac­tion. That gives us a solu­tion in 19 min­utes (as illus­trat­ed by the gif below!).

 

1

If my excel­lent art­work did­n’t make sense, here’s a table explain­ing what happened.

Side A	Side B	Time Elapsed
1M, 2M, 5M, 10M	X	0 Min­utes
5M, 10M	1M, 2M	2 Min­utes
1M, 5M, 10M	2M	3 Min­utes
10M	1M, 2M, 5M	8 Min­utes
1M, 10M	2M, 5M	9 Min­utes
X	1M, 2M, 5M, 10M	19 Min­utes

So that gets us at a mod­est 19 min­utes, but actu­al­ly we can do bet­ter. Instead of mak­ing 1M run all over the place, we’re going to give him a break on Side B. The issue with the above solu­tion is that we’re wast­ing a total of 15 minute get­ting 10M and 5M across. Ide­al­ly, you’d like 10M and 5M to go across togeth­er to mit­i­gate the lost time, but still make it so that one of them does­n’t have to walk back.

The below gif illus­trates the opti­mal solu­tion of 17 minutes.

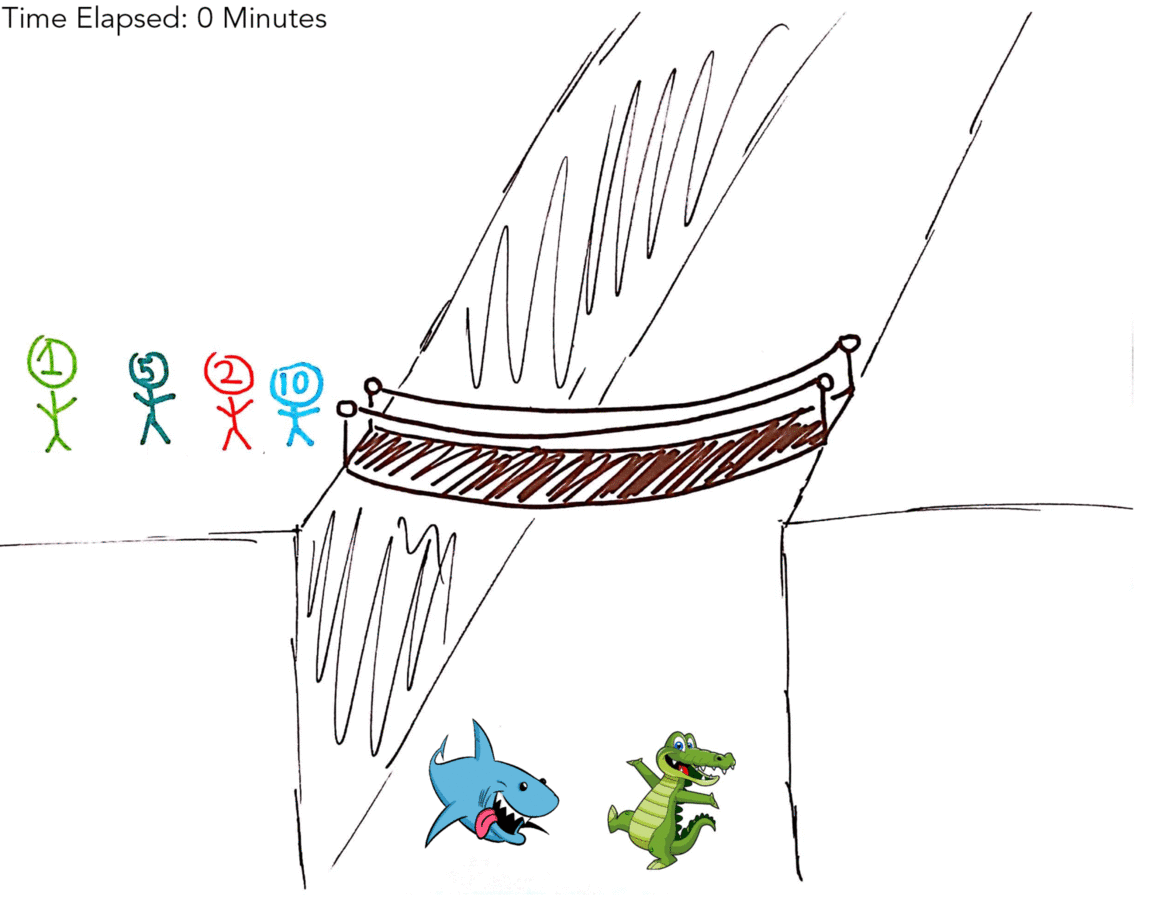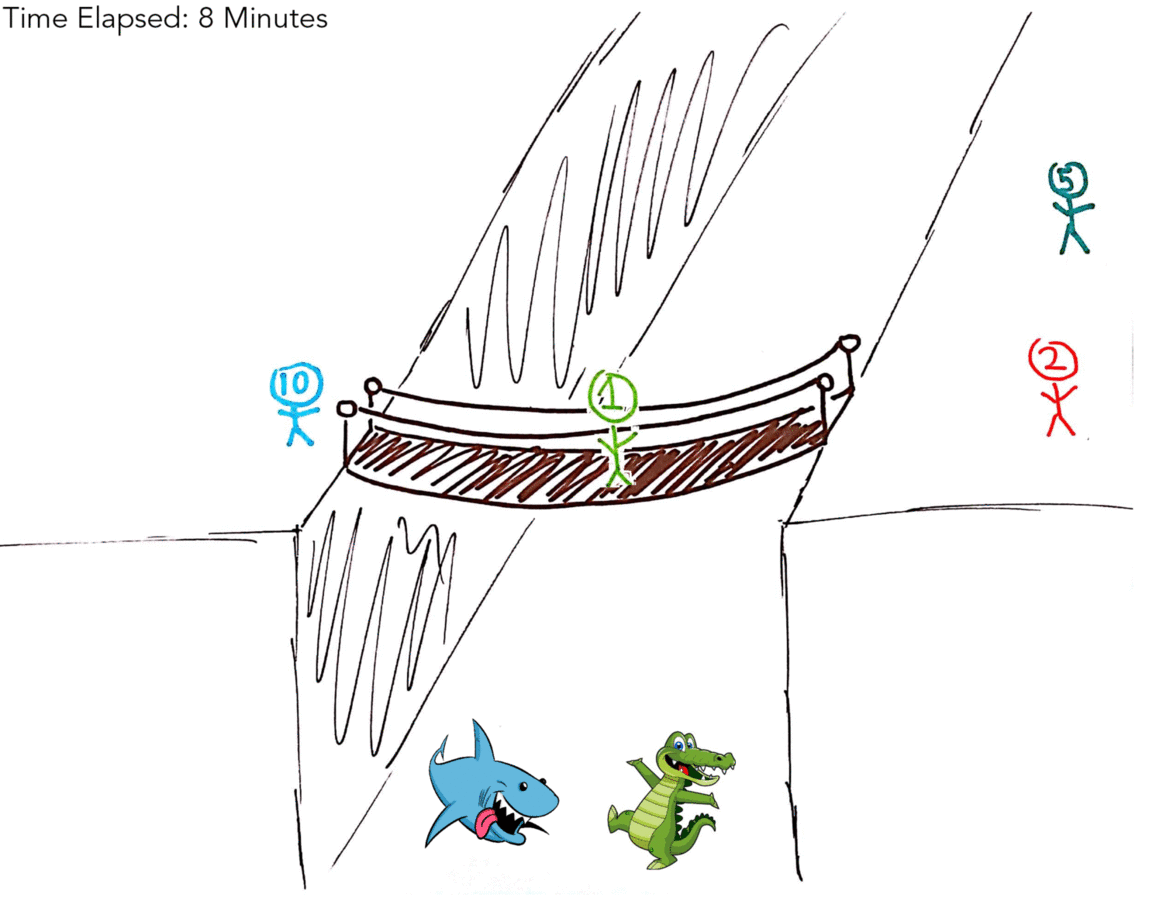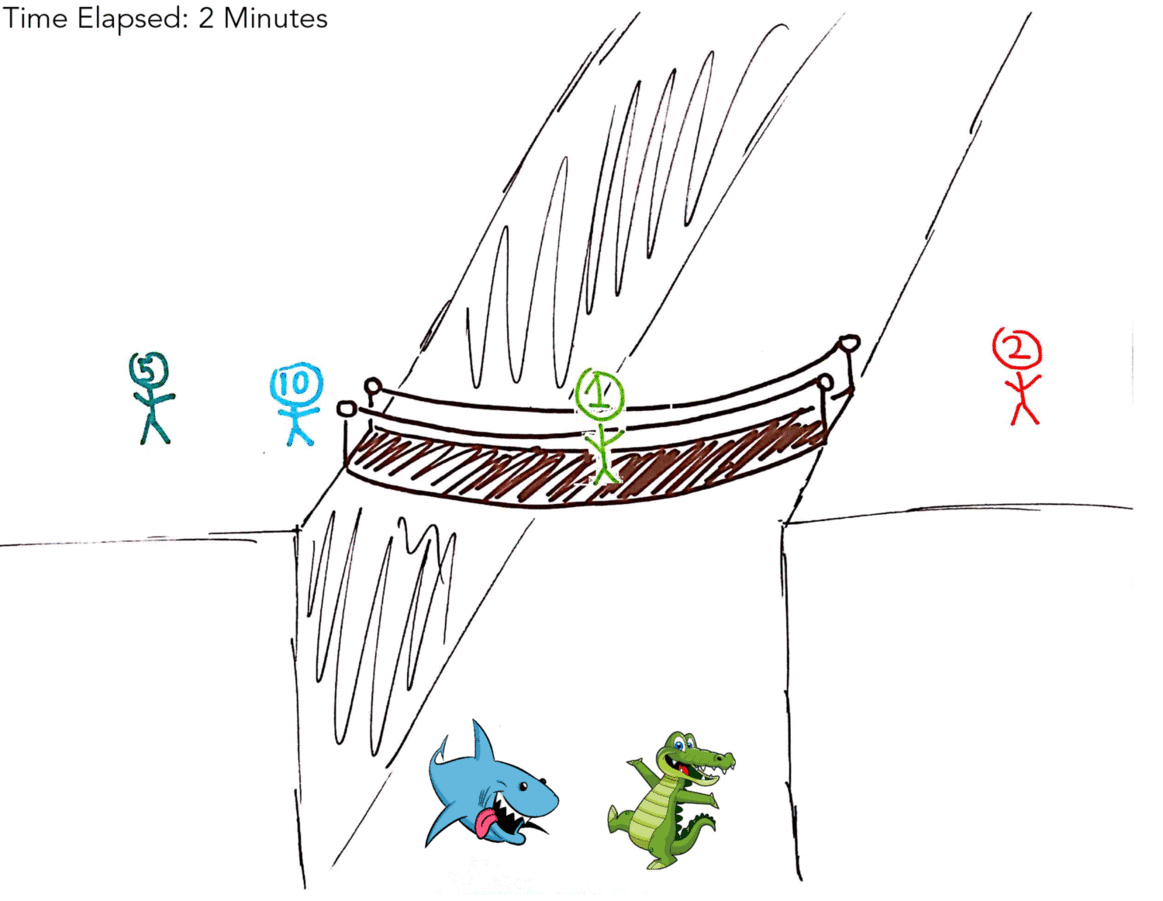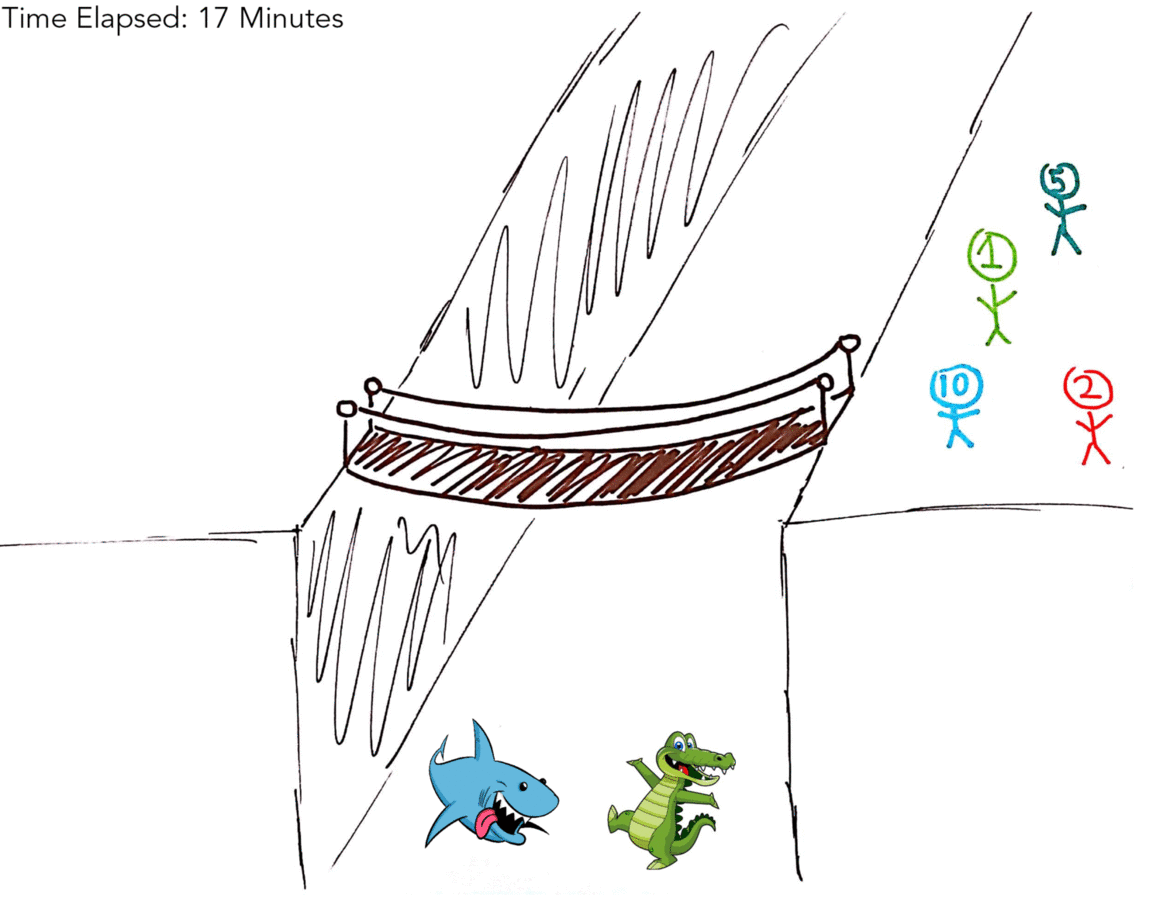
Again, if that did­n’t make sense here’s a table:

 

Side A	Side B	Time Elapsed
1M, 2M, 5M, 10M	X	0 Min­utes
5M, 10M	1M, 2M	2 Min­utes
1M, 5M, 10M	2M	3 Min­utes
1M	2M, 5M, 10M	13 Min­utes
1M, 2M	5M, 10M	15 Min­utes
X	1M, 2M, 5M, 10M	17 Min­utes

 

You can see here that we were able to save time by mak­ing 5M & 10M go over togeth­er with­out mak­ing one of them walk back, giv­ing the opti­mal solu­tion of 17 min­utes.